之前计划学习「深度学习」相关内容,于是我在JD上买了很多和这个主题有关的书,其中就包括这篇文章推荐的「Python神经网络编程」。
为什么我在标题中,称其为"入门神经网络的儿童读本"呢? 因为同时期我还买了一本书,深度学习(DEEP LEARNING),由于封面是一个花园,所以它一般也被称为"花书"。花书大约500页,每页都是密密麻麻的字,和一堆数学公式,如果你计划直接阅读花书来入门深度学习的话,就相当于让一个刚识字的孩子直接去看四大名著,可能字都认识,连起来不明白它到底想表达什么意思。
而这本书200多页,一共22多万字,分为3个主要章节和2个附录,由于文字浅显易懂,读起来不会有太多障碍,因此一个周末的时间就能读完。看这本书,相当于让孩子在直接读四大名著前,先看注音白话版(含插画),先增加自信心,提起后续继续的阅读的兴趣。
举个例子,在「深度学习」和「Python神经网络编程」都有一个关于XOR(异或)的案例,用于说明线性分类器(线性模型: y=ax+b)的局限性。在读「深度学习」的时候,我只是知道XOR不行,但是不知道为什么作者要举XOR这个例子。而「Python神经网络编程」的作者解决了我这个疑惑。
下图中,我们可以发现AND和OR能够使用一条直线,根据输入x1和x2判断输出是0还是1.
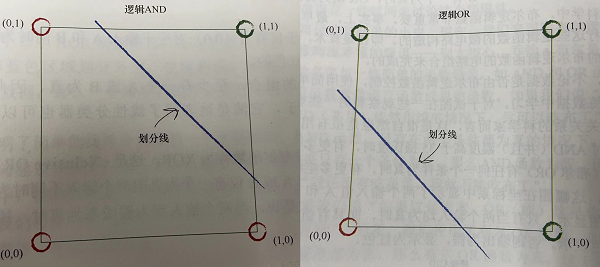
但是对于XOR,你无法借助于一条直线将图中的红色和绿色点进行区分,所以为什么不去试试神奇的"神经网络"呢?
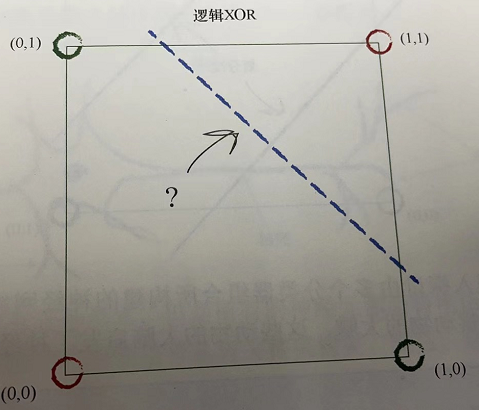
另外一个例子,就是我理解了为什么线性代数在神经网络中那么重要。在「Python神经网络编程」的1.7节中,作者先带着我们一步一步在神经网络中追踪信号的传递, 先计算了第二层的第一个节点,也就是x=(第一个节点的输出 * 链接权重 ) + (第二个节点的输出 * 链接权重),然后再按照相同的思路计算了其他节点。在1.7节的最后,作者说到
...好在,即使是面对一个具有很多层,众多节点的神经网络,数学可以帮助我们以非常简洁的方式写下计算出所有输出值的命令。由于这种简洁性,指令变得非常短,执行起来也更有效率,因此这种简洁性不仅仅是对人类读者有益处,对计算机而言,也一样大有裨益。这一简洁方式就是使用矩阵...
在1.8节中,作者引入了矩阵的计算方式,然后将之前的繁琐的计算过程化简成 $X = W \cdot I$, 使得我知其然并知其所以然。
最后,我花了3天晚上把这本书看完了,让我从"花书"的打击中走了出来。这一幕就跟当年不知好歹,想通过「算法导论」 入门算法一样,最后还是靠着「图解算法」活了过去。

