两个序列之间的距离,定义为平均每个核苷酸置换的期望数。
计算距离是最简单的思路就是看两个序列的相异度,也就是不同的核苷酸占整体的比例. 然而这种思路只能处理高度相似的情况 > 95%, 因为序列在进化过程中,存在反复横跳的情况,也就是 A->T->A, 或者A->T->C->G->A, 也就是核苷酸很有可能经历了多次置换.
为了描述这种状态,我们需要用到马尔科夫链,它是一种随机过程,当前的状态(state)只取决于上一个状态(state), 和更早的状态无关。用公式化的语言,表述如下
$$
P(X=x_n|X=x_,X=x_,...) =P(X=X_n|X=x_)
$$
在书的1.2节中, 作者从开始最简单的JC69模型开始介绍距离估计中的马尔科夫模型。 在书中,作者引入了一个置换率矩阵(subsitution-rate matrix)的概念,并说道 「这里,核苷酸按T, C, A和G的顺序,矩阵的每一行总和为0,任意一个核苷酸i的总置换率为 3$\lambda$, 记为$-q_$.
刚开始读这段的时候,没有觉得不对劲,仿佛我都看懂了一样。但是,再次阅读到这里的时候,我脑中就闪现一个问题,为什么每一行总和要是0?谁规定的呢?
为了解决这个问题,我就检索了 substituion-rate matrix 这个关键词。但是结果要么是BLOSUM这种替换频率矩阵,要么就返回JC69模型的置换矩阵。
进一步,我想这个概念是不是来自于马尔科夫链。于是我搜索了中文和英文,得到矩阵都是概率转换矩阵(transition matrix),行和是1,而不是0.
不过山重水复疑无路,柳暗花明又一村,在我查到这篇文章时Nucleotide substitution models,我觉得这篇文章写的特别好,进一步,我发现了这个网站还发布了其他教程,其中一篇就是Understanding Continuous-Time Markov Models, 我终于明白原来书里的马尔科夫链指的是Continuous-time Markov chain, CTMC, 而我之前脑中的马尔科夫链是一个离散过程(DTMC)。
随后,我去找了相关的视频,比较详细的是Lecture 4: Continuous time Markov chains, 如下是我总结的一些知识点
- CTMC和DTMC一样,定义是当前时刻的状态只受前一刻时间的影响,同时后续讨论的CTMC还要求时间同质,即只要间隔时间相同,转移概率矩阵也相同
- DTMC只需要一个概率转移矩阵,但是CTMC得要无限个,因为有无数种可能的时间间隔
- 那么CTMC能否只通过一个矩阵描述呢?基于Chapman-Kolmogorov theorm和矩阵线性微分返程求解,发现可以通过rate matrix(Q)来算出任一时间间隔的转移概率, 即P(t)=exp(Qt)。 Q也可以称之为generator matrix.
- Q中的元素q_xy表示从x变成y所需要的速率。
- Q的性质1,根据q_xy的定义, 当x!=y时, q_xy >= 0, 否则会算出负数概率
- Q的性质2,计算Q矩阵的行和为0, 因此q_xx 为负。
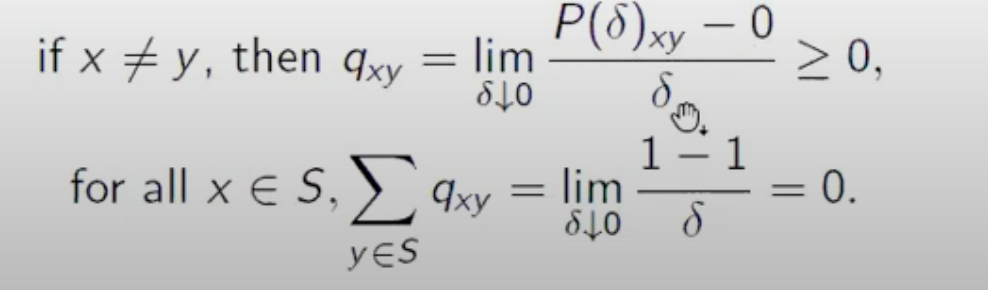
计算分子进化这本书涉及到的数学基础有点多,看来要恶补了。
