第9章 ArchR的拟混池重复
因为scATAC-seq数据本质上只有两种值,也就是说每个位点要么开放要么不开放,所以你会发现某些情况下无法使用单个细胞进行数据分析。此外,许多我们想要做的分析也依赖于重复才能计算统计显著性。对于单细胞数据,我们通过构建拟混池重复(pseudo-bulk replicates)来解决该问题。所谓的拟混池(pesudo-bulk)指的就是将单细胞进行合并模拟成混池测序的ATAC-seq实验得到的数据。ArchR为每个目标细胞分组构建多个拟混池样本,也就得到了拟混池重复。这个模拟过程背后的假设是将单细胞进行合并结果和实际的混池结果非常接近,以至于不需要在乎背后的差异。这些细胞分组通常都是来自于单个细胞类群,或者是一直细胞类型对应的可能聚类。我们这一章会介绍如何使用ArchR生成这些拟混池重复。
9.1 ArchR如何构建拟混池重复
ArchR使用分级优先法(tiered priority approach)构建拟混池重复。使用者定义: i)最小和最大重复数(minReps/maxReps), ii)每个重复的最少和最多细胞数(minCells/maxCells), iii)缺少足够细胞用于构建足够重复时的采样率(Sampling Ratio)。举个例子,当采样率等于0.8时,每个重复中80%的细胞来自于无放回抽样(这会导致重复间出现有放回抽样)。在这种情况下,多个重复中可能有一些相同的细胞,但是为了能在缺少足够细胞的分组里得到拟混池重复,这是必要的牺牲。
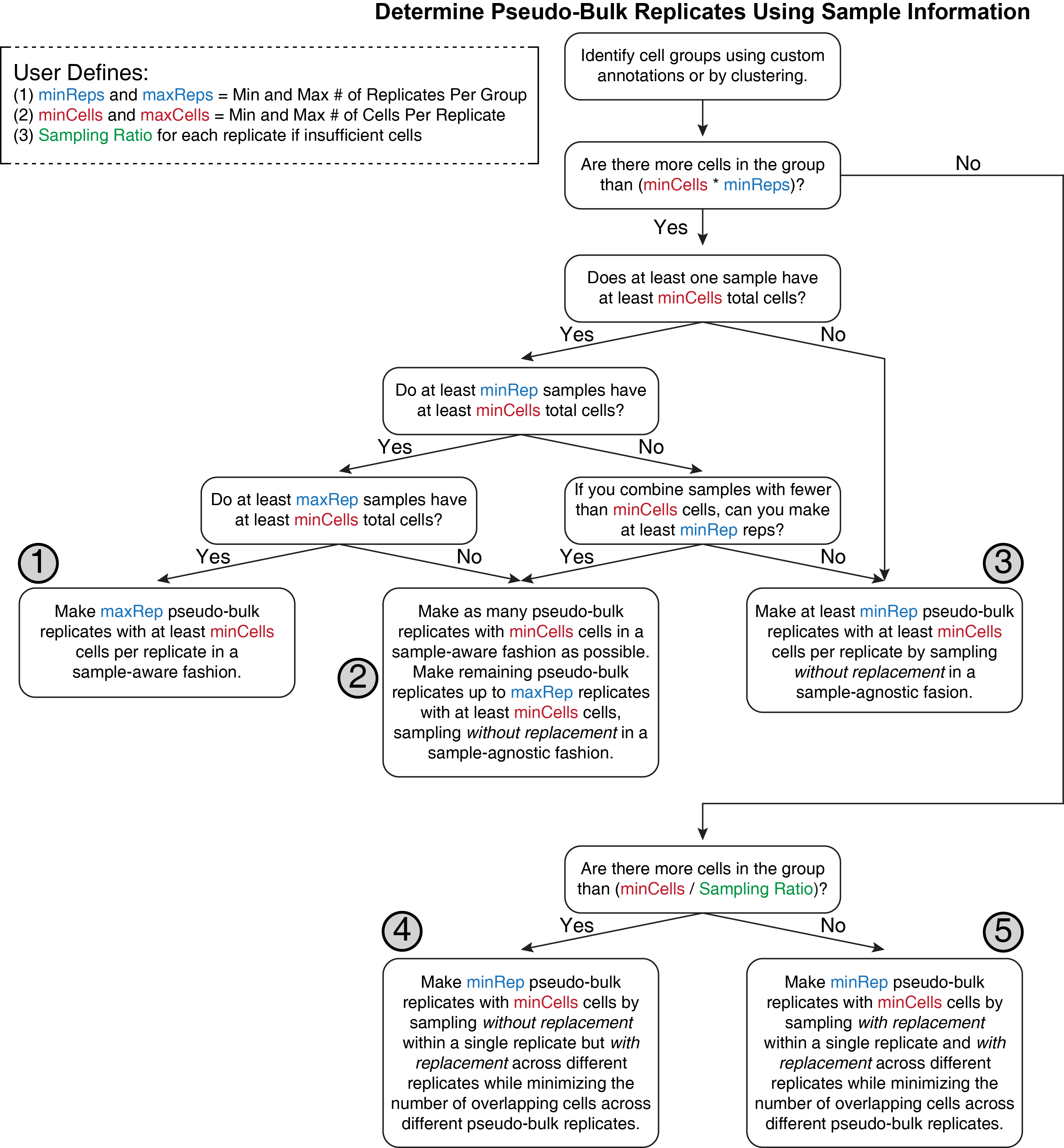
我们的拟混池重复生成过程可以用如下的决策树进行描述

流程有些复杂,这里概述下这个流程中的几个关键注意事项。
首先,用户确定细胞的分组,ArchR通常会称之为聚类,我们可以在第五章分析分析得到。
其次,对于每一组,ArchR尝试去创建理想的拟混池重复。所谓理想的拟混池重复,指的是每个重复只有一个样本构成,这就要求每个样本得保证足量的细胞数。这样保证了重复间的样本多样性和生物学变异,是ArchR所期望得到的最佳结果,但这一过程实际上会有5种可能的结果,根据ArchR的偏好排序如下
- 数据拥有足够多的样本(至少要等于maxRep定义的重复),且每个样本的细胞数都大于
minCell, 于是每个样本都可以作为拟混池重复,每个重复的细胞都来自于同一个样本。 - 一些样本的细胞数超过
minCell,因此能够单独形成一个重复。剩下的重复则是通过将余下的细胞进行混合,然后通过无放回抽样得到。 - 数据里没有一个样本的细胞数超过
minCell, 但是总细胞数超过minCells * minReps。因此将所有的细胞进行混合,然后进行无放回抽样,抽样时不考虑细胞来源。 - 一个细胞分组中的总细胞数低于
minCells * minReps,但是大于minCells / Sample Ratio。此时单个样本的构建采取无放回抽样,重复间则需要有放回抽样,降低多个拟混池重复间的相同细胞数。 - 一个细胞分组中的总细胞数低于
minCells / Sample Ratio。这意味着我们必须在单个重复和跨重复中都采取有放回抽样策略。这是最糟糕的情况,后续在使用这些拟混池重复做下游分析分析要特别小心。后续可以通过设置ArchR的minCells参数进行淘汰。
我们使用如下的数据集阐述这一过程
Sample Cluster1 Cluster2 Cluster3 Cluster4 Cluster5
A 800 600 900 100 75
B 1000 50 400 150 25
C 600 900 100 200 50
D 1200 500 50 50 25
E 900 100 50 150 50
F 700 200 100 100 25
我们设置的参数为minRep=3,maxRep=5, minCells=300, maxCells=1000和sampleRatio=0.8,也就是最少有3个重复,最多是5个重复,每个重复至少有300个细胞,最多是1000个细胞,当细胞数不满住要求,抽样率设置为0.8.
9.1.1 Cluster1
对于Cluster1, 我们的6个样本(大于maxRep)的细胞数都高于minCells(300)。这是最理想的情况,对应上述第一种情况,我们将会得到5个拟混池重复,保证每个重复都来自独立的样本。
Rep1 = 800 cells from SampleA
Rep2 = 1000 cells from SampleB
Rep3 = 1000 cells from SampleD
Rep4 = 900 cells from SampleE
Rep5 = 700 cells from SampleF
对于这些重复,我们需要注意两个事情:(1) 因为我们的样本数足够多,能够保证每个重复都来自独立的样本,所以可以淘汰其中细胞数最少的SampleC。(2)由于maxCells设置为1000,因此最多只能有1000个细胞。
9.1.2 Cluster2
对于Cluster2, 我们有3个样本的细胞数超过minCells, 另外3个样本的细胞数都不够。这对应上述第二种情况,我们会以如下的方法构建拟混池重复。
Rep1 = 600 cells from SampleA
Rep2 = 900 cells from SampleC
Rep3 = 500 cells from SampleD
Rep4 = 350 cells [50 cells from SampleB + 100 from SampleE + 200 from SampleF]
在这个例子中,Rep4由其他几个样本的细胞混合后通过无放回抽样得到
9.1.3 Cluster3
对于Cluster3,我们只有两个样本超过minCells, 不满足minReps。但是如果我们将剩余的样本的细胞进行混合形成额外的重复,它的细胞数就超过了minCells。最终我们得到了3个拟混池重复,对应上述的情况3。我们将得到如下重复
Rep1 = 900 cells from SampleA
Rep2 = 400 cells from SampleB
Rep3 = 250 cells [100 cells from SampleC + 50 from SampleD + 50 from SampleE + 50 from SampleF]
和Cluster2类似,Cluster3的Rep3由其他几个样本的细胞混合后通过无放回抽样得到
9.1.4 Cluster4
对于Cluster4,总细胞数是570个,小于minCells * minReps(900). 在这个情况下,我们无法保证有足够多的细胞通过无放回抽样的方式保证每个重复都有最小的细胞数。但是,总的细胞数依旧依旧大于minCells / sampleRatio(375个细胞),这意味着每个重复中细胞可以来自于无放回抽样,重复之间的细胞需要放回抽样。这对应着上述的情况4,我们将得到如下重复
Rep1 = 300 cells [250 unique cells + 25 cells overlapping Rep2 + 25 cells overlapping Rep3]
Rep2 = 300 cells [250 unique cells + 25 cells overlapping Rep1 + 25 cells overlapping Rep3]
Rep3 = 300 cells [250 unique cells + 25 cells overlapping Rep1 + 25 cells overlapping Rep2]
在这个情况中,ArchR会尽可能降低任意两个拟混池重复的相同细胞。
9.1.5 Cluster5
对于Cluster5,总共是250个细胞,同时小于minCells * minReps(900)和minCells / sampleRatio(375). 这意味着每个样本都需要有放回的抽样,重复之间也需要有放回抽样,才能得到拟混池重复。这是上述说到的第5种情况,是其中最糟糕的情况。对于这类拟混池重复,在后续的分析中需要谨慎使用。我们将得到如下的重复:
Rep1 = 300 cells [250 unique cells + 25 cells overlapping Rep2 + 25 cells overlapping Rep3]
Rep2 = 300 cells [250 unique cells + 25 cells overlapping Rep1 + 25 cells overlapping Rep3]
Rep3 = 300 cells [250 unique cells + 25 cells overlapping Rep1 + 25 cells overlapping Rep2]
9.2 构建拟混池重复
通过上一节了解ArchR构建拟混池重复的逻辑后,我们就可以开始实际操作了。在ArchR中,我们通过调用addGroupCoverages()函数来构建拟混池重复。它的关键参数groupBy,定义了拟混池重复需要使用的分组。这里我们用的是上一章scRNA-seq数据标记的细胞类型,也就是Cluster2
projHeme4 <- addGroupCoverages(ArchRProj = projHeme3, groupBy = "Clusters2")
得到这些拟混池重复后,我们就能从数据中鉴定peak了。就像之前所说的,我们不希望使用所有的细胞鉴定peak,而是单独根据每一组细胞(例如聚类)单独鉴定peak,这样才有可能分析出不同组的特异性peak。这一章得到数据就为后续鉴定peak提供了良好的开始。